APLICACIÓN DE LAS FUNCIONES EN LA ARQUITECTURA

FUNCIÓN

Una función es como una máquina: tiene una entrada y una salida. Lo que sale está relacionado de alguna manera con lo que entra

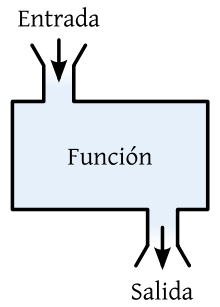El nombre más común es "f", pero puedes ponerle otros como “g, n, d, k” o hasta "mermelada" si quieres. Una función relaciona cada elemento de un conjunto con un elemento exactamente de otro conjunto (puede ser el mismo conjunto).

Como componentes que integran una función está el conjunto "X" que es el dominio, el conjunto "Y" que es el codo-minio, y el conjunto de elementos de Y a los que llega alguna flecha (los valores verdaderos de la función) se denomina rango o imagen.

Concluyendo rápidamente lo que es una función están lo siguiente:

·         Una función relaciona entradas con salidas.

·         Una función toma elementos de un conjunto (dominio) y los relaciona con elementos de otro conjunto (codo-minio).

·         Las salidas (los verdaderos valores de la función) se denominan imagen o rango.

·         Una entrada sólo produce una salida.

·         Una entrada y la salida ubicándolos juntos se nombran par ordenado.

·         Así que una función también se puede ver como un conjunto de pares ordenados.

-PROPIEDADES DE UNA FUNCIÓN

·         Signo de la función. Dada un función f(x), determinar su signo es hallar para qué valores del dominio es f(x) < 0 y f(x) > 0

·         Ceros de la función. Son los valores del dominio que son las soluciones de la ecuación f(x) = 0.

·         Monotonía. Es la variación de la función respecto a la variable independiente x. Comprende los conceptos de crecimiento y decrecimiento.

·         Puntos extremos. Son los puntos más altos y más bajos de la gráfica de una función. Un máximo de una

·         Acotación. Una función se dice acotada cuando el recorrido está entre dos valores y por lo tanto su gráfica estará entre dos rectas.

·         Simetría. Las simetrías de las funciones nos van a facilitar su representación gráfica. Una función se dice par si se cumple para todos los puntos del dominio que f(x) = f (-x). Una función se dice impar si se cumple para todos los puntos del dominio que f (-x) = -f(x).

·         Periodicidad. Una función es periódica si se repite cada cierto intervalo de amplitud T. Es decir, que se cumple que para todo el dominio que f(x) = f(x + T). Al valor T se le llama período.

-OPERACIONES CON FUNCIONES

Al igual que los números, las funciones pueden realizar operaciones algebraicas. En todos los casos debemos tener cuidado con los dominios de las funciones que participan en la operación y de la función resultado de la operación.

·         Suma de funciones:                                (f + g) (x) = f(x) + g(x).

·         Diferencia de funciones:                         (f - g) (x) = f(x) - g(x).

·         Producto de funciones:                           (f∙g) (x) = f(x) ∙g(x).

                                            

·         Cociente de funciones:              

                                                                 

·         Composición de funciones. Esta es una operación especial que se utiliza mucho para crear nuevas funciones. Componer dos funciones es aplicar una de ellas sobre la imagen de la otra. Se debe tener cuidado con los dominios

CLASIFICACIÓN DE FUNCIONES

FUNCIONES ALGEBRAICAS

En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.

·         Funciones explícita: Se pueden obtener las imágenes de x por simple sustitución

·         Funciones implícitas: No se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.

Funciones Polinómicas: Vienen definidas por un polinomio, su dominio es R

Funciones Racionales: Viene dado por un cociente entre polinomio. El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.

FUNCIONES TRASCENDENTE

En las funciones trascendentes la variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

Función Exponencial: De la forma f(x) = ax .Donde a y x son números reales tal que a> 0 y a es diferente de uno, puede considerarse como la inversa de la función logarítmica en cuanto se cumpla que:  

Propiedades:

·         La función aplicada al valor cero es siempre igual a 1: f (0) = a⁰ = 1.

·         La función exponencial de 1 es siempre igual a la base: f (1) = a¹ = a.

·         La función exponencial de una suma de valores es igual al producto de la aplicación de dicha función aplicada a cada valor por separado.

f (x + x?) = a^x+x? = a^x × a^x? = f (x) × f (x?).

·         La función exponencial de una resta es igual al cociente de su aplicación al minuendo dividida por la función del sustraendo:

f (x - x?) = a^x-x? = a^x/a^x? = f (x)/f (x?).

Un caso particular de la función exponencial es f (x) = e^x El número e, de valor 2,7182818285..., se define matemáticamente como el límite al que tiende la expresión:    (1 + 1/n)ⁿ

APLICACIÓN DE LA FUNCIÓN EXPONENCIAL

El matemático Weidman dedujo la base para la construcción de la torre. Un factor crucial para los cálculos que Eiffel tenía en mente pasaba por calibrar el efecto de las fuerzas ejercidas por el viento sobre determinados puntos estructurales de la Torre. La clave para su solución deriva de dos ecuaciones exponenciales diferentes interconectadas: una para la mitad superior de la torre, y otra en la que interviene el factor de sobre-dimensionamiento  de seguridad de la estructura en su base.

  

     

APLICACIÓN DE MATRICES EN LA ARQUITECTURA

En matemáticas, una matriz es un arreglo rectangular de números que pueden sumarse, restarse, multiplicarse, que se usan generalmente para describir sistemas de ecuaciones (lineales y diferenciales) o representar una aplicación lineal.

En arquitectura, una matriz es la forma de organizar cierto número de datos en un formato de tal manera que puedan relacionarse entre sí. Una matriz es dependiente de la relación que tenga con el entorno del edificio o el espacio donde se integre, también puede ser utilizada para indicar el grado de atracción o repelencia entre locales de un edificio.

APLICACIÓN DE LAS CÓNICAS EN LA ARQUITECTURA

Las cónicas constituyen uno de los conjuntos de curvas más importantes de la Geometría y que se utilizan en distintas ramas, una de ellas es la arquitectura. Se denomina como sección cónica, a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano.

El matemático griego Menecmo descubrió estas curvas y fue el matemático griego Apolonio de Perga el primero en estudiar detalladamente las curvas cónicas y encontrar la propiedad plana que las definía. Apolonio descubrió que las cónicas se podían clasificar en tres tipos a los que dio el nombre de: Elipse, Hipérbola y Parábola

ELIPSE

Es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante. La elipse se encuentra formando parte de la imagen que de algunos edificios como son:

-El Coliseo de Roma es sin duda el edificio más simbólico de la ciudad, y junto al Vaticano, la imagen de Roma en el mundo, el contorno del coliseo constituye la forma de una elipse.